Understanding the geometry of a cube is essential for anyone interested in mathematics, engineering, or design. One of the most fundamental questions in this context is: how many vertices does a cube have? This article will delve into this topic, providing a detailed explanation and exploring related concepts to enhance your understanding of cube geometry.
A cube is a three-dimensional shape with specific properties that make it one of the most studied geometric figures. Its vertices, edges, and faces play a crucial role in defining its structure. By the end of this article, you'll not only know the number of vertices in a cube but also gain insights into its other geometric properties.
Whether you're a student, educator, or simply someone curious about mathematics, this article will provide you with all the information you need. Let's explore the fascinating world of cube geometry together!
Read also:Deven Tell Unveiling The Multifaceted Talent And Inspiring Journey
Table of Contents
- Introduction to Cubes
- What Are Vertices?
- How Many Vertices Does a Cube Have?
- Properties of a Cube
- Cube Vertices and Edges
- Mathematical Formula for Cube Vertices
- Real-World Applications
- Common Questions About Cube Vertices
- Cube Vertices in Computer Graphics
- Historical Significance of Cubes
- Conclusion
Introduction to Cubes
A cube is a three-dimensional solid object bounded by six square faces, with three meeting at each vertex. It is one of the five Platonic solids and is widely recognized for its symmetry and regularity. The cube is a perfect example of a polyhedron, which is a three-dimensional shape with flat polygonal faces, straight edges, and vertices.
Cubes are not only fascinating from a mathematical perspective but also have practical applications in various fields, including architecture, engineering, and computer graphics. Understanding the properties of a cube, such as its vertices, edges, and faces, is essential for anyone working with three-dimensional shapes.
What Are Vertices?
Vertices are the points where two or more edges of a geometric shape meet. In simpler terms, they are the corners of a shape. For example, in a triangle, there are three vertices, while in a square, there are four. Vertices play a crucial role in defining the structure of a shape and are essential for calculations involving geometry and topology.
When discussing three-dimensional shapes like cubes, vertices become even more important. They help determine the spatial orientation of the shape and are used in various mathematical and computational applications.
How Many Vertices Does a Cube Have?
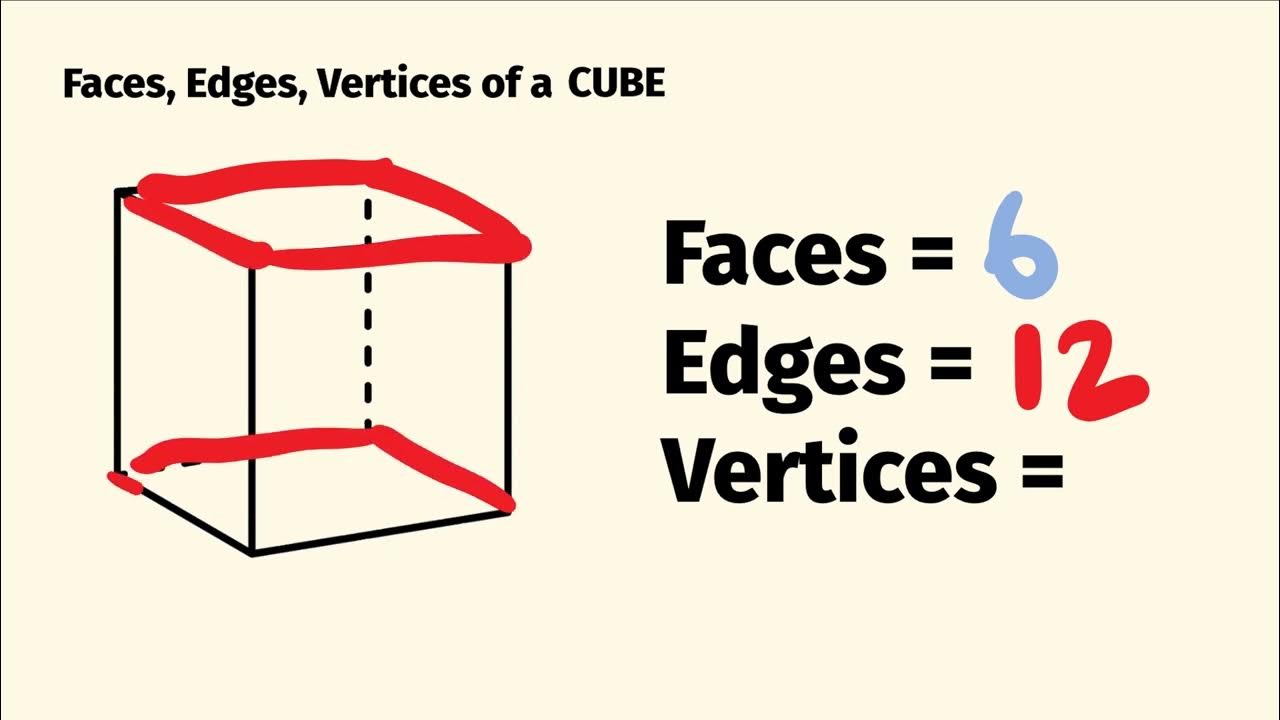
A cube has 8 vertices. This is one of the defining characteristics of a cube and can be easily verified by examining its structure. Each vertex of a cube is formed by the intersection of three edges, and there are eight such points in total.
Understanding the number of vertices in a cube is fundamental to studying its geometry. It helps in solving problems related to volume, surface area, and spatial relationships. Additionally, knowing the number of vertices is essential for applications in computer graphics and engineering.
Read also:How Much Is Cheryl Cole Worth A Comprehensive Look At Her Net Worth And Career Achievements
Properties of a Cube
A cube is a highly symmetrical shape with several distinct properties:
- Six Faces: A cube has six square faces, each of which is congruent and perpendicular to its adjacent faces.
- Twelve Edges: There are twelve edges in a cube, each of which connects two vertices.
- Eight Vertices: As discussed earlier, a cube has eight vertices, where three edges meet at each point.
- Equal Dimensions: All edges of a cube are of equal length, making it a regular polyhedron.
These properties make the cube a unique and fascinating geometric shape with numerous applications in both theoretical and practical fields.
Cube Vertices and Edges
Relationship Between Vertices and Edges
The relationship between vertices and edges in a cube is governed by Euler's formula for polyhedra:
V - E + F = 2
Where:
- V: Number of vertices
- E: Number of edges
- F: Number of faces
For a cube, substituting the known values:
8 (vertices) - 12 (edges) + 6 (faces) = 2
This confirms the validity of Euler's formula for a cube, further reinforcing the mathematical consistency of its structure.
Mathematical Formula for Cube Vertices
While there isn't a specific formula solely for calculating the number of vertices in a cube, the properties of a cube can be derived from its definition as a regular polyhedron. By examining the intersection of edges and the symmetry of the shape, we can deduce that a cube has exactly eight vertices.
In more complex geometric shapes, formulas like Euler's can be used to calculate vertices, edges, and faces. However, for a cube, the number of vertices is a well-known and fixed value.
Real-World Applications
Cubes have numerous practical applications across various fields:
- Architecture: Cubic structures are commonly used in building design due to their stability and symmetry.
- Engineering: Engineers often use cube-shaped components in construction and manufacturing processes.
- Computer Graphics: Cubes are fundamental building blocks in 3D modeling and rendering.
- Mathematics: The cube serves as a basis for understanding more complex geometric shapes and relationships.
These applications highlight the importance of understanding cube geometry, including the number of vertices, in real-world scenarios.
Common Questions About Cube Vertices
Here are some frequently asked questions about cube vertices:
- What is the difference between vertices and edges? Vertices are the points where edges meet, while edges are the line segments connecting vertices.
- Can a cube have more than eight vertices? No, a standard cube always has exactly eight vertices.
- How are vertices used in computer graphics? Vertices define the corners of 3D models, enabling the creation of complex shapes and animations.
These questions and answers provide clarity on common misconceptions and deepen the understanding of cube geometry.
Cube Vertices in Computer Graphics
In computer graphics, cubes are often represented using vertices, edges, and faces. Each vertex is defined by its coordinates in three-dimensional space, and the connections between vertices form the edges and faces of the cube. This representation allows for efficient rendering and manipulation of 3D objects in virtual environments.
Modern software tools and programming languages, such as OpenGL and DirectX, provide robust support for working with cube vertices. By understanding the mathematical properties of a cube, developers can create realistic and visually appealing graphics for games, simulations, and other applications.
Historical Significance of Cubes
Cubes have been studied for thousands of years, with early civilizations recognizing their symmetry and regularity. The ancient Greeks, in particular, were fascinated by the cube and considered it one of the five Platonic solids. These shapes were believed to represent the fundamental elements of the universe.
Today, cubes continue to be an important subject of study in mathematics, science, and art. Their properties and applications have expanded far beyond their historical roots, making them an indispensable part of modern technology and design.
Conclusion
In conclusion, understanding the geometry of a cube, including the number of vertices, is essential for anyone interested in mathematics, engineering, or design. A cube has eight vertices, twelve edges, and six faces, making it a highly symmetrical and versatile shape. By exploring the properties and applications of cubes, we gain valuable insights into the world of geometry and its practical implications.
We encourage you to share this article with others who may find it informative. If you have any questions or comments, please feel free to leave them below. Additionally, explore our other articles on mathematics and geometry to deepen your knowledge and appreciation of these fascinating subjects.
References:
![How many faces edges and vertices does a cube have[solved]](https://d138zd1ktt9iqe.cloudfront.net/media/seo_landing_files/cube-1614171313.png)